use the is-lm model to determine what happens to the equilibrium
xvi.25 The IS-LM Model
The IS-LM model provides another style of looking at the determination of the level of brusque-run real gdp (real Gross domestic product) in the economy. Like the aggregate expenditure model, information technology takes the toll level as fixed. But whereas that model takes the interest charge per unit as exogenous—specifically, a change in the interest rate results in a change in autonomous spending—the IS-LM model treats the involvement charge per unit equally an endogenous variable.
The basis of the IS-LM model is an analysis of the coin market and an analysis of the goods market, which together make up one's mind the equilibrium levels of involvement rates and output in the economic system, given prices. The model finds combinations of interest rates and output (GDP) such that the money market place is in equilibrium. This creates the LM curve. The model likewise finds combinations of involvement rates and output such that the goods market is in equilibrium. This creates the IS curve. The equilibrium is the interest charge per unit and output combination that is on both the IS and the LM curves.
LM Curve
The LM bend represents the combinations of the interest rate and income such that money supply and coin demand are equal. The need for money comes from households, firms, and governments that use money equally a means of exchange and a store of value. The police force of demand holds: equally the involvement rate increases, the quantity of money demanded decreases because the interest charge per unit represents an opportunity cost of holding money. When interest rates are higher, in other words, money is less effective as a store of value.
Money demand increases when output rises because money also serves every bit a medium of exchange. When output is larger, people have more income and so desire to agree more money for their transactions.
The supply of money is called by the budgetary dominance and is independent of the interest rate. Thus information technology is drawn as a vertical line. The equilibrium in the money market is shown in Figure 16.17 "Coin Market Equilibrium". When the coin supply is chosen by the monetary authorisation, the interest rate is the toll that brings the market into equilibrium. Sometimes, in some countries, central banks target the money supply. Alternatively, fundamental banks may choose to target the interest charge per unit. (This was the case we considered in Chapter x "Understanding the Fed".) Effigy xvi.17 "Coin Market Equilibrium" applies in either example: if the monetary authority targets the interest rate, and then the money market tells us what the level of the money supply must be.
Figure 16.17 Money Marketplace Equilibrium
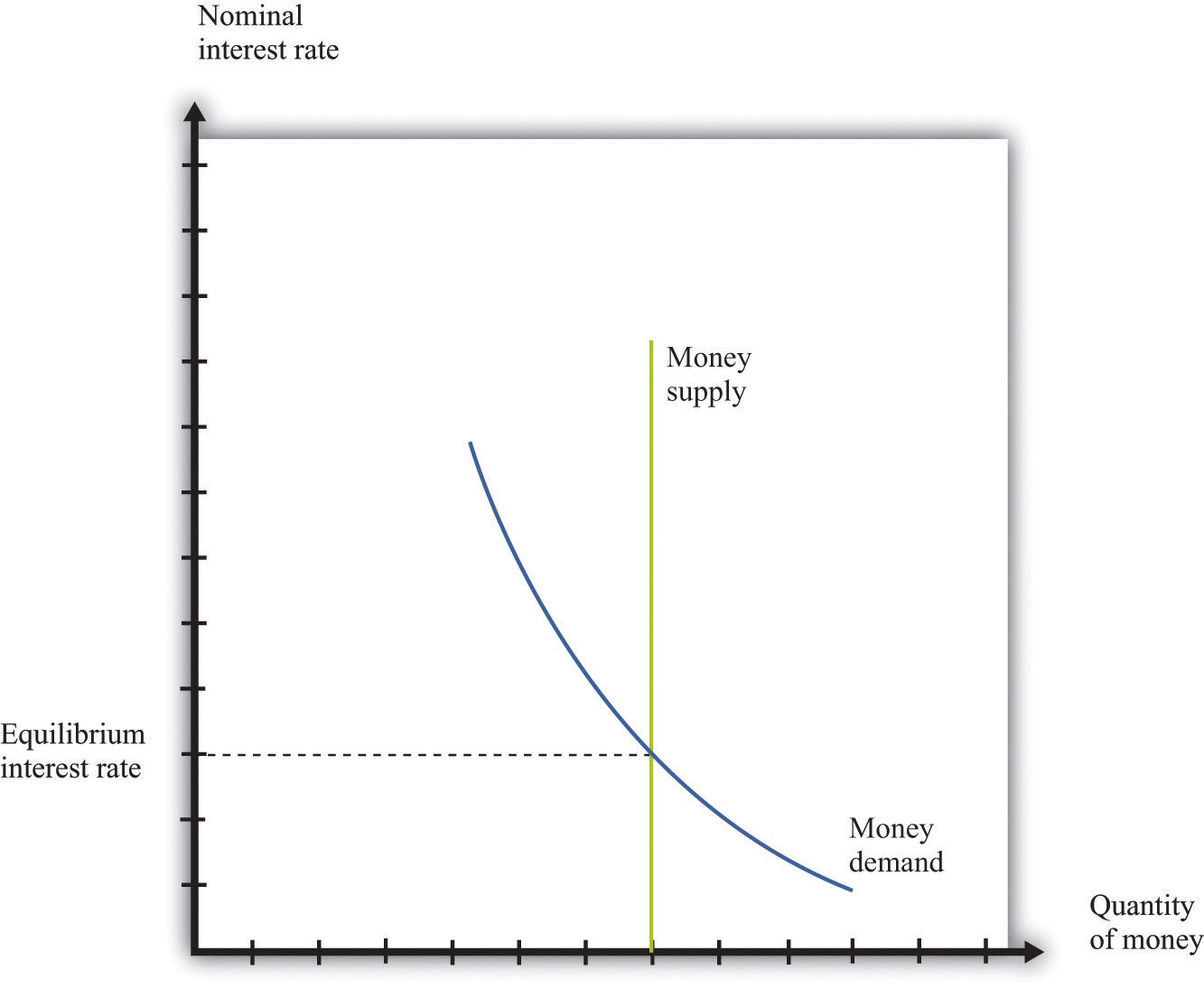
To trace out the LM curve, nosotros await at what happens to the involvement rate when the level of output in the economy changes and the supply of money is held fixed. Effigy 16.18 "A Change in Income" shows the coin market place equilibrium at 2 unlike levels of real GDP. At the higher level of income, money demand is shifted to the correct; the involvement rate increases to ensure that coin need equals money supply. Thus the LM bend is upward sloping: higher real GDP is associated with higher interest rates. At each point along the LM curve, money supply equals money demand.
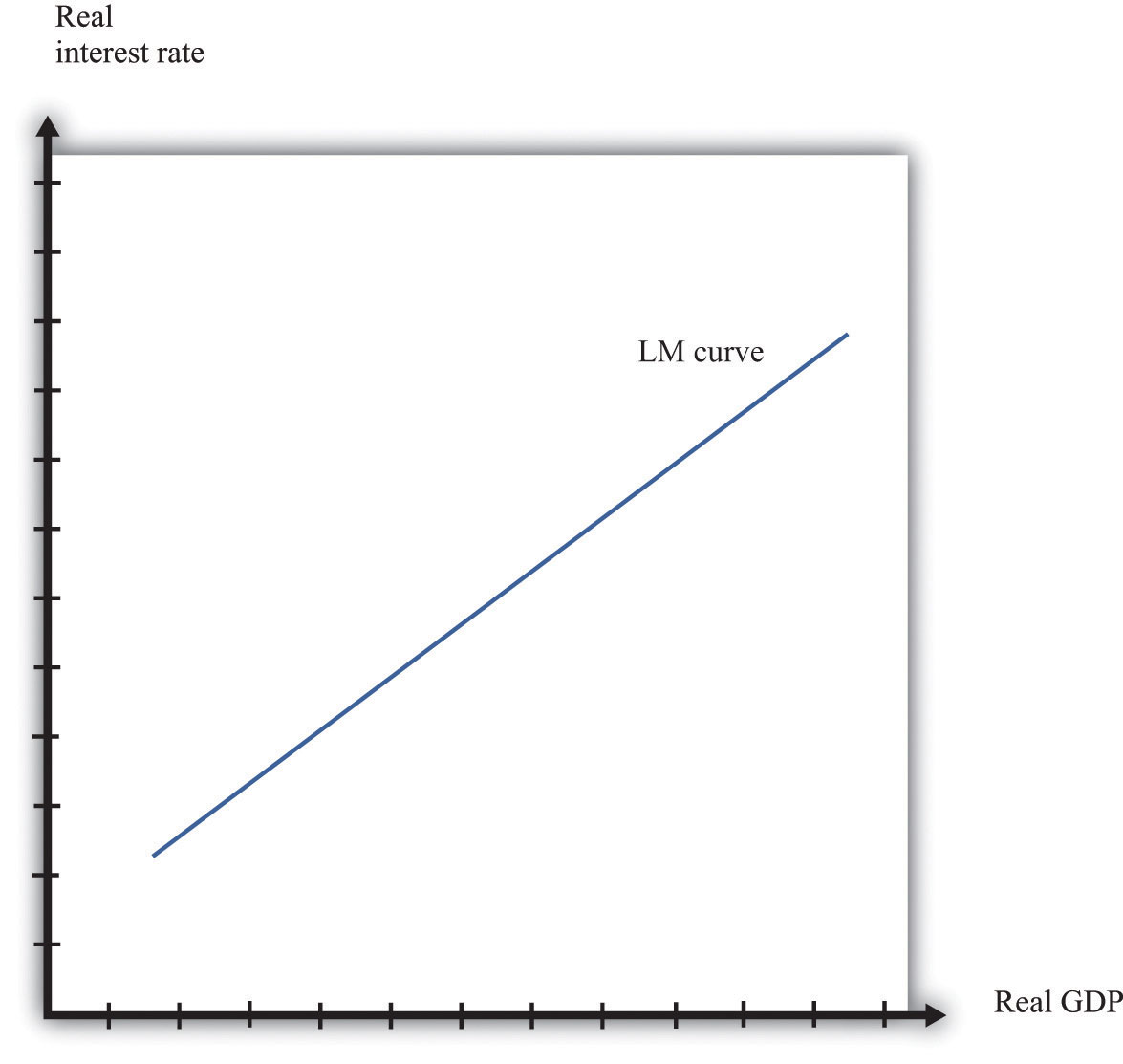
Nosotros take not yet been specific about whether we are talking nearly nominal interest rates or real interest rates. In fact, information technology is the nominal interest rate that represents the opportunity cost of holding money. When we depict the LM bend, however, nosotros put the real interest rate on the axis, every bit shown in Effigy 16.19 "The LM Curve". The simplest way to remember nigh this is to suppose that nosotros are considering an economy where the aggrandizement rate is zippo. In this case, by the Fisher equation, the nominal and real interest rates are the same. In a more complete analysis, we tin incorporate aggrandizement by noting that changes in the inflation rate will shift the LM curve. Changes in the money supply also shift the LM curve.
Figure sixteen.18 A Change in Income
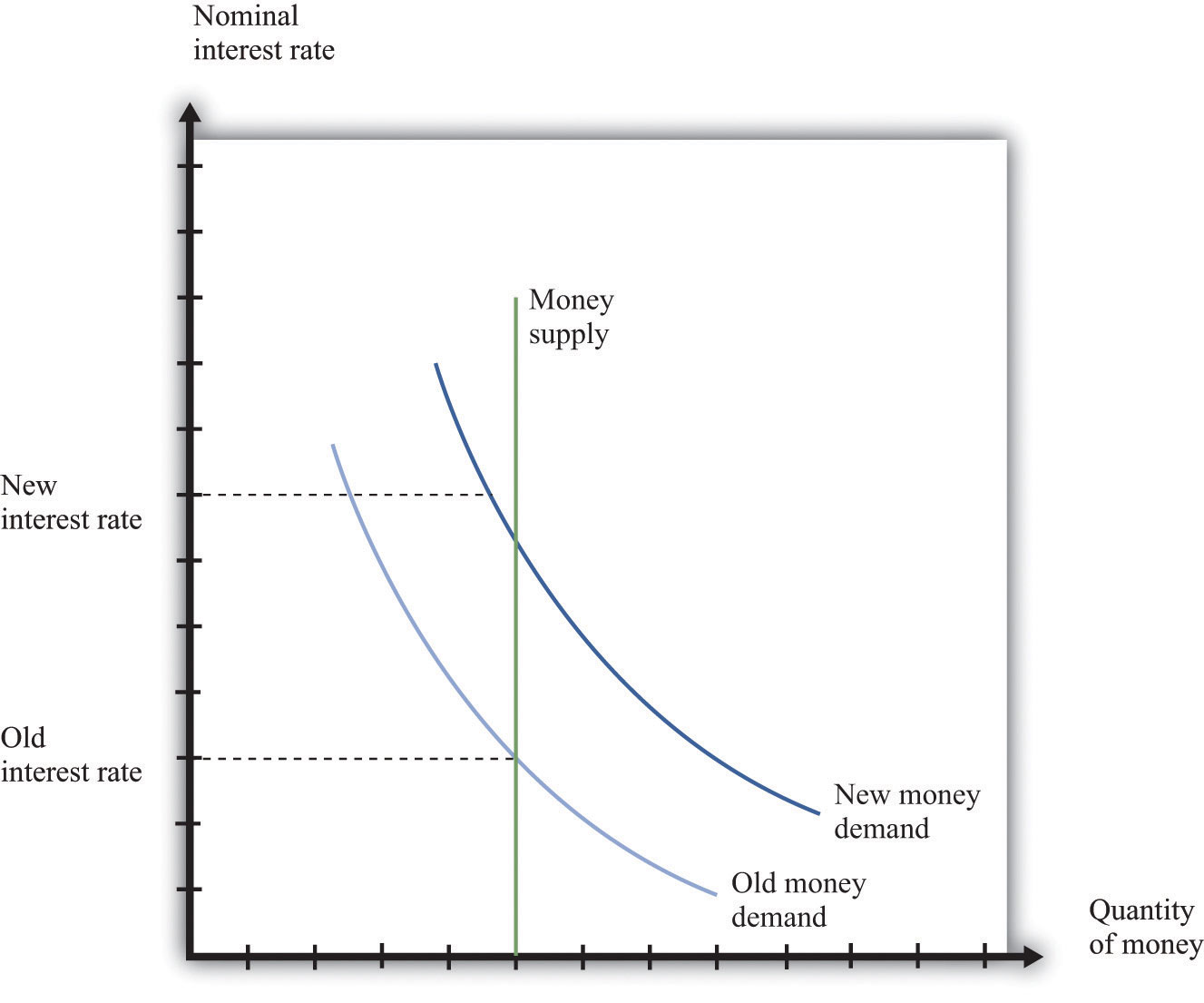
Figure 16.19 The LM Curve
IS Curve
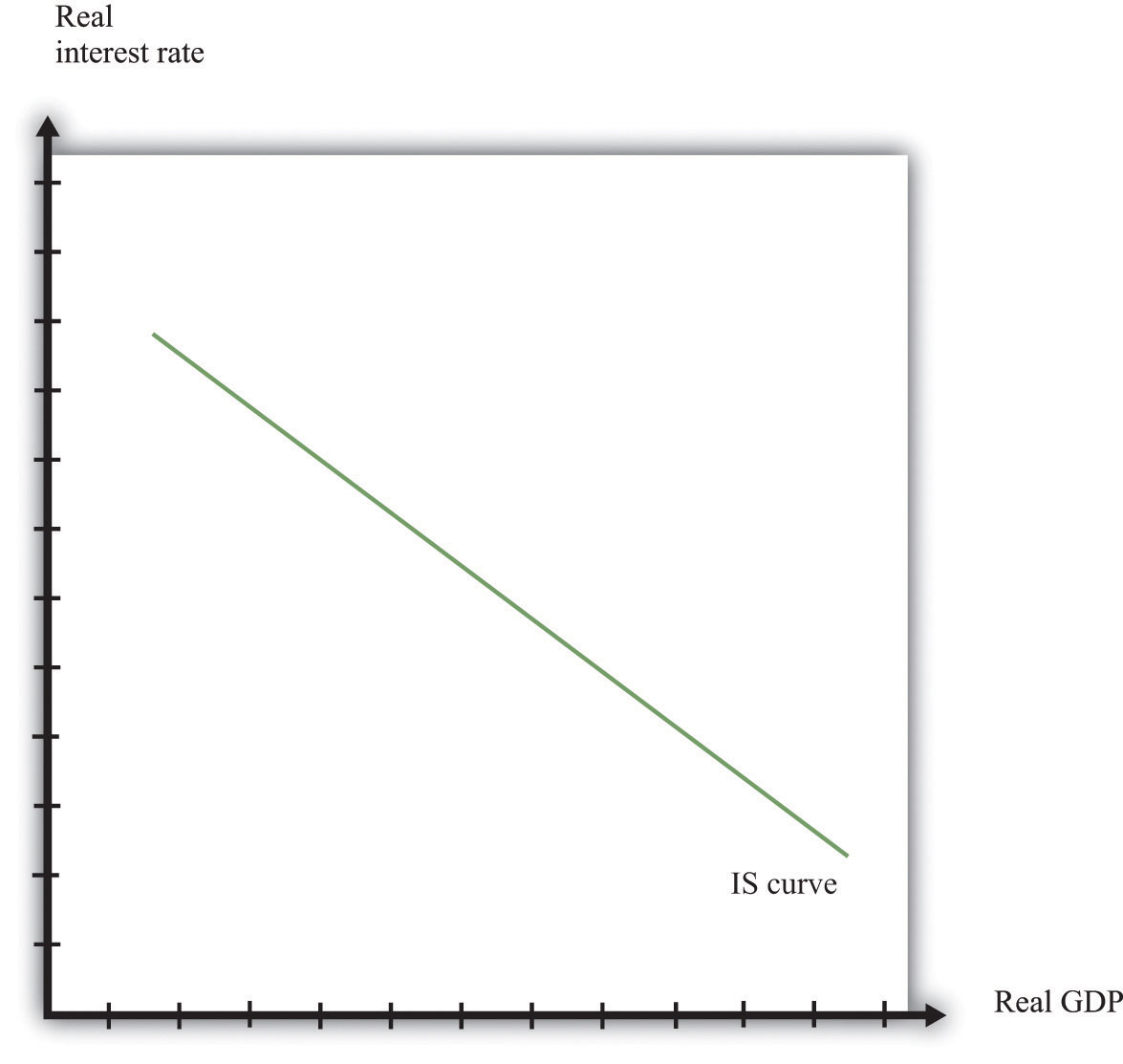
The IS curve relates the level of real GDP and the real involvement rate. It incorporates both the dependence of spending on the real interest rate and the fact that, in the short run, real GDP equals spending. The IS curve is shown in Effigy 16.eighteen "A Change in Income". Nosotros label the horizontal centrality "real Gdp" since, in the short run, real Gross domestic product is determined by amass spending. The IS curve is downward sloping: equally the real interest rate increases, the level of spending decreases.
Effigy 16.20 The IS Curve
In fact, we derived the IS curve in Chapter 10 "Agreement the Fed". The dependence of spending on real involvement rates comes partly from investment. As the existent interest rate increases, spending by firms on new majuscule and spending by households on new housing decreases. Consumption also depends on the real involvement rate: spending by households on durable appurtenances decreases as the existent interest charge per unit increases.
The connection between spending and real GDP comes from the aggregate expenditure model. Given a particular level of the interest charge per unit, the aggregate expenditure model determines the level of existent Gross domestic product. At present suppose the interest rate increases. This reduces those components of spending that depend on the interest charge per unit. In the aggregate expenditure framework, this is a reduction in democratic spending. The equilibrium level of output decreases. Thus the IS curve slopes downwards: higher interest rates are associated with lower real GDP.
Equilibrium
Combining the give-and-take of the LM and the IS curves will generate equilibrium levels of interest rates and output. Note that both relationships are combinations of interest rates and output. Solving these two equations jointly determines the equilibrium. This is shown graphically in Figure xvi.21. This just combines the LM curve from Effigy sixteen.xix "The LM Curve" and the IS bend from Effigy 16.twenty "The IS Bend". The crossing of these two curves is the combination of the involvement rate and real Gross domestic product, denoted (r*,Y*), such that both the money market place and the appurtenances market are in equilibrium.
Figure xvi.21
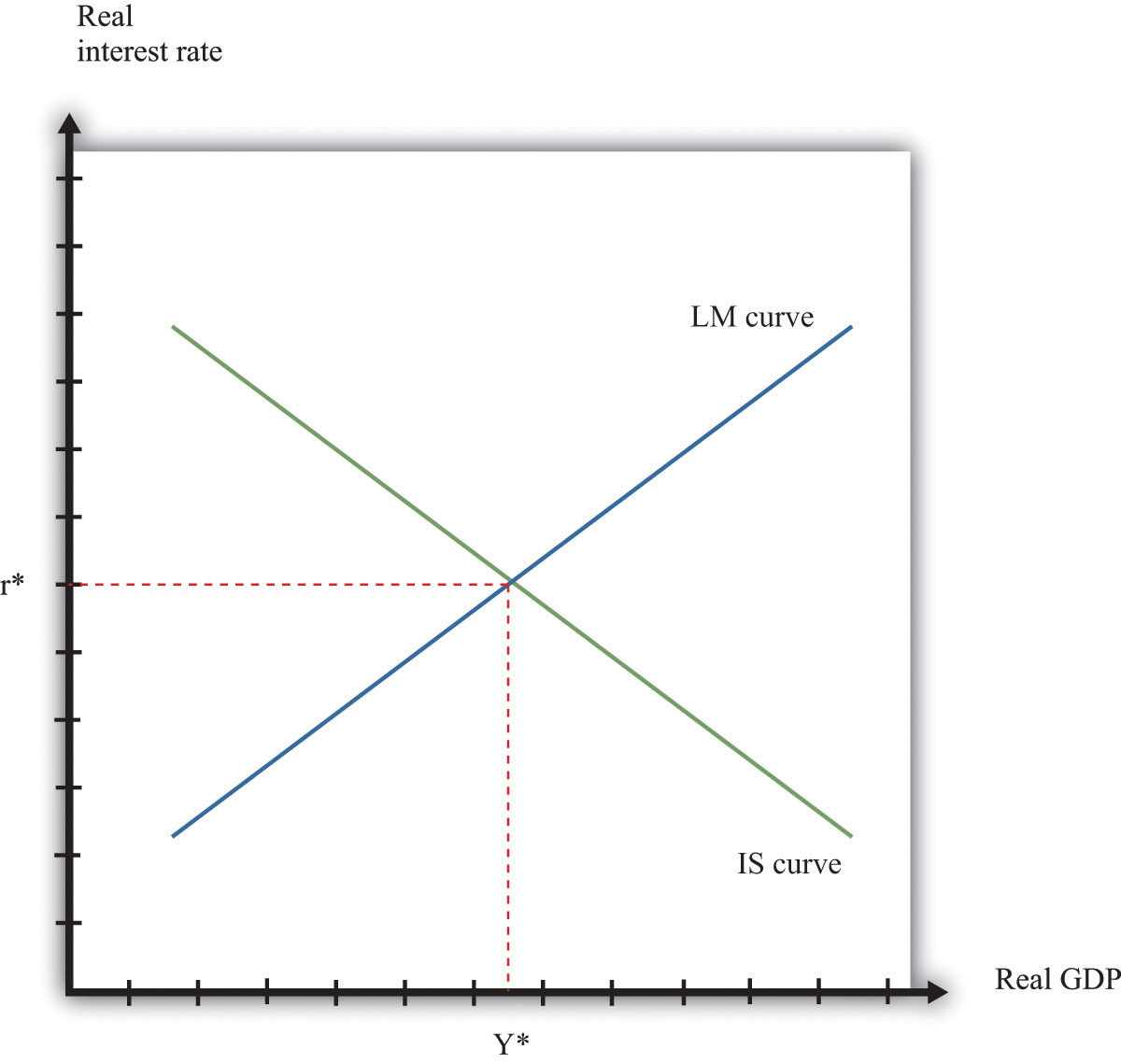
Equilibrium in the IS-LM Model.
Comparative Statics
Comparative statics results for this model illustrate how changes in exogenous factors influence the equilibrium levels of interest rates and output. For this model, there are ii key exogenous factors: the level of autonomous spending (excluding any spending afflicted by interest rates) and the real coin supply. We can written report how changes in these factors influence the equilibrium levels of output and involvement rates both graphically and algebraically.
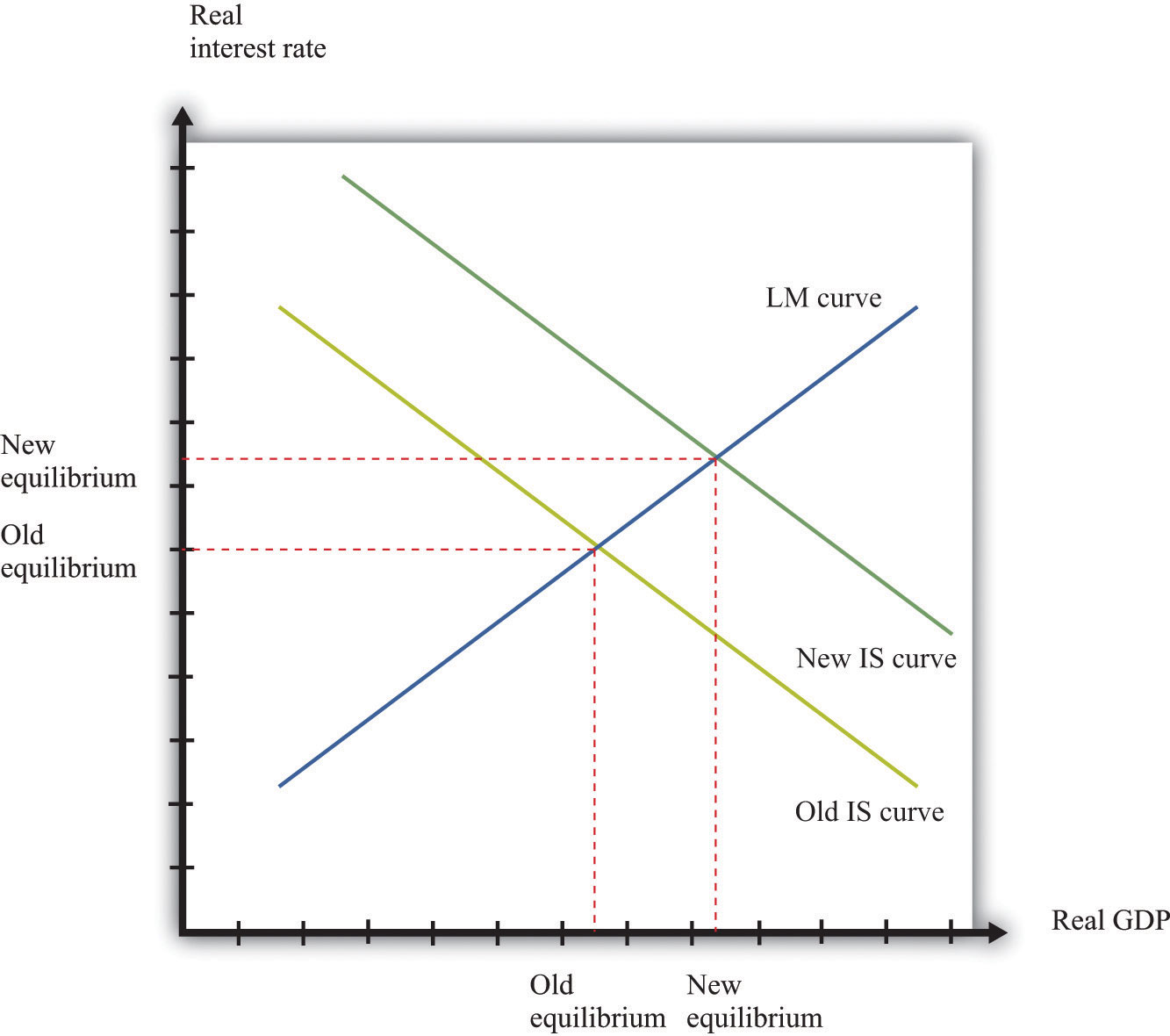
Variations in the level of autonomous spending will lead to a shift in the IS curve, every bit shown in Figure 16.22 "A Shift in the IS Curve". If autonomous spending increases, then the IS curve shifts out. The output level of the economic system volition increase. Interest rates ascension equally we move forth the LM curve, ensuring money market equilibrium. One source of variations in democratic spending is fiscal policy. Autonomous spending includes government spending (Thousand). Thus an increase in G leads to an increase in output and involvement rates every bit shown in Figure sixteen.22 "A Shift in the IS Curve".
Figure 16.22 A Shift in the IS Curve
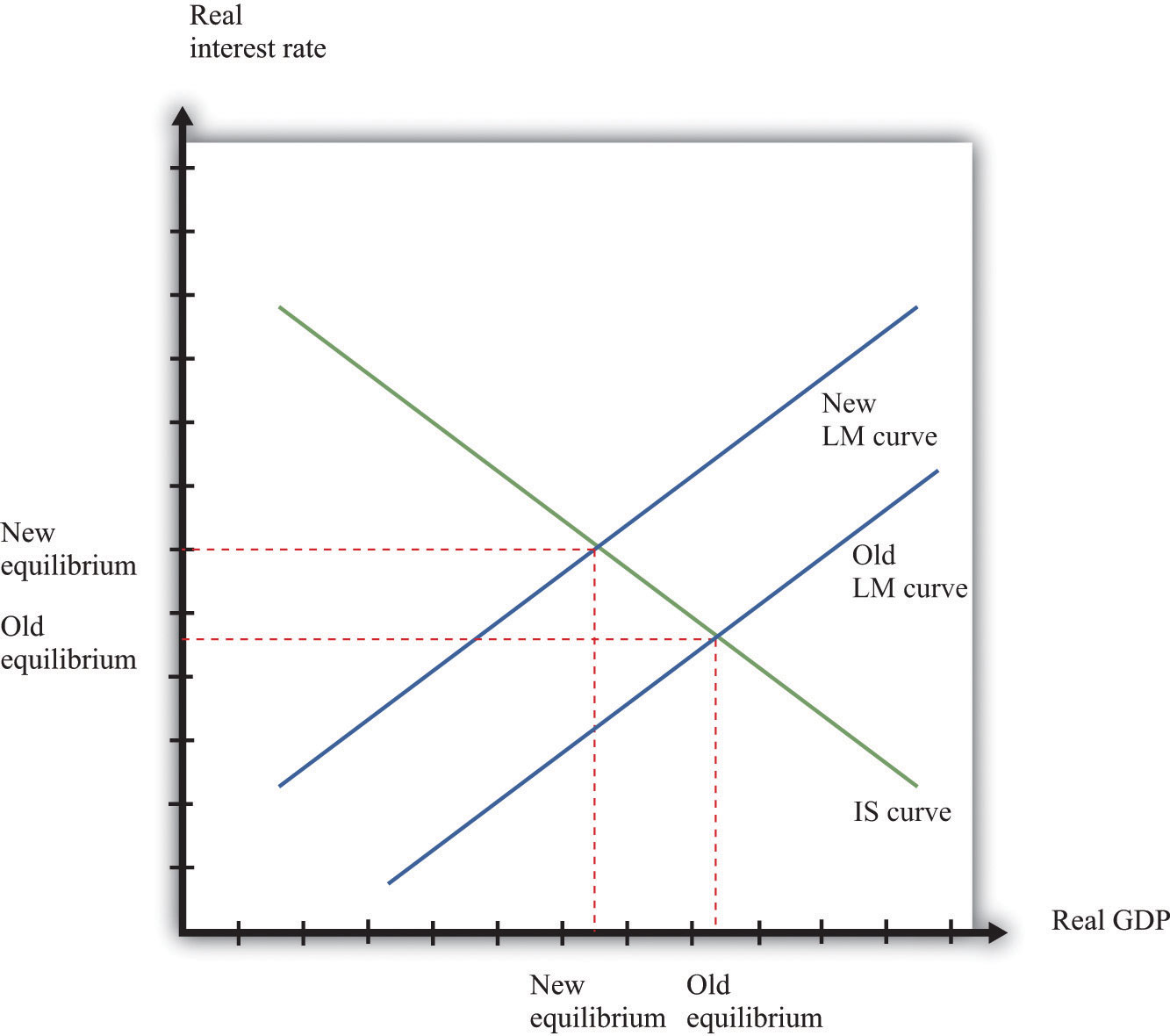
Variations in the existent coin supply shift the LM bend, as shown in Figure sixteen.23 "A Shift in the LM Curve". If the money supply decreases, then the LM bend shifts in. This leads to a higher real interest charge per unit and lower output as the LM bend shifts along the fixed IS curve.
Figure 16.23 A Shift in the LM Curve
More Formally
We can represent the LM and IS curves algebraically.
LM Curve
Let L(Y,r) stand for real money need at a level of existent GDP of Y and a real involvement rate of r. (When we say "real" money demand, we mean that, as usual, we have deflated by the toll level.) For simplicity, suppose that the inflation rate is zero, so the real interest rate is the opportunity cost of holding money.If we wanted to include aggrandizement in our assay, we could write the existent demand for money equally L(Y, r + π), where π is the inflation rate. Assume that real money demand takes a particular form:
L(Y,r) = L0 + 50ane Y – Ltwo r.
In this equation, Fifty0, Lone, and Ltwo are all positive constants. Real money demand is increasing in income and decreasing in the interest rate. Letting M/P exist the real stock of money in the economic system, then coin market place equilibrium requires
M/P = L0 + L1Y – L2 r.
Given a level of real GDP and the real stock of coin, this equation tin exist used to solve for the involvement rate such that coin supply and money need are equal. This is given by
r = (i/502) [L0 + L1Y – 1000/P].
From this equation we larn that an increase in the existent stock of money lowers the interest rate, given the level of real GDP. Further, an increase in the level of real GDP increases the interest rate, given the stock of money. This is another way of saying that the LM curve is upward sloping.
IS Curve
Recall the 2 equations from the aggregate expenditure model:
Y = Due east
and
Due east = E 0(r) + βY.
Hither we have shown explicitly that the level of autonomous spending depends on the real interest rate r.
We tin solve the 2 equations to find the values of E and Y that are consistent with both equations. We notice
Given a level of the real interest rate, nosotros solve for the level of autonomous spending (using the dependence of consumption and investment on the real interest charge per unit) and so employ this equation to find the level of output.
Here is an example. Suppose that
C = 100 + 0.6Y, I = 400 − 5r, G = 300,
and
NX = 200 − 0.1Y,
where C is consumption, I is investment, Thou is government purchases, and NX is net exports. First group the components of spending as follows:
C + I + K + NX = (100 + 400 − vr + 300 + 200) + (0.6Y − 0.iY)
Adding together the starting time group of terms, we detect autonomous spending:
E 0 = 100 + 400 + 300 + 200 − 5r = thou − fiver.
Adding the coefficients on the income terms, we find the marginal propensity to spend:
β = 0.six − 0.1 = 0.5.
Using β = 0.5, nosotros calculate the multiplier:
We so calculate real Gdp, given the existent interest charge per unit:
Y = two × (k − 5r) = 2000 − 10r.
Equilibrium
Combining the discussion of the LM and the IS curves will generate equilibrium levels of interest rates and output. Note that both relationships are combinations of interest rates and output. Solving these two equations jointly determines the equilibrium.
Algebraically, we accept an equation for the LM curve:
r = (i/Fifty2) [L0 + Fifty1 Y – One thousand/P].
And we have an equation for the IS bend:
Y = mE 0(r),
where we let m = (1/(1 – β)) denote the multiplier. If nosotros presume that the dependence of spending in the interest charge per unit is linear, so that East 0(r) = e0 – due east1 r, and then the equation for the IS curve is
Y = m (e0-eastwardane r),
To solve the IS and LM curves simultaneously, nosotros substitute Y from the IS curve into the LM curve to get
r = (ane/L2) [Fifty0 + Fifty1 m(due east0-east1 r) – M/P].
Solving this for r we get
r = A r – B r M/P.
where both A r and B r are constants, with A r = (L0 + L1 me 0)/(L1 me 1 + L2) and Br = one/(L1 me one + 50two). This equation gives us the equilibrium level of the real interest rate given the level of autonomous spending, summarized by eastward 0, and the real stock of money, summarized by M/P.
To discover the equilibrium level of output, nosotros substitute this equation for r dorsum into the equation for the IS curve. This gives the states
Y = A y + B y(1000/P),
where both A y and B y are constants, with A y = thou(e 0 – e i A r) and B y = me 1 B r. This equation gives u.s. the equilibrium level of output given the level of autonomous spending, summarized past e 0, and the real stock of money, summarized by Yard/P.
Algebraically, we tin employ the equations to make up one's mind the magnitude of the responses of involvement rates and output to exogenous changes. An increase in the autonomous spending, e 0, will increase both A r and A y, implying that both the interest rate and output increase.To see that Ay increases with e 0 requires a bit more algebra. An increase in the real coin stock will reduce interest rates by B r and increase output by B y. A key part of monetary policy is the sensitivity of spending to the interest rate, given by e one. The more than sensitive is spending to the involvement rate, the larger is east 1 and therefore the larger is B y.
Source: https://saylordotorg.github.io/text_macroeconomics-theory-through-applications/s20-25-the-is-lm-model.html